เรือยนต์ลำหนึ่งแล่นไปตามแม่น้ำผ่านแพที่จุด A จากนั้นอีก 60 นาที เรือจึงแล่นกลับมา และผ่านแพอีกครั้งที่ระยะห่าง 6.0 กิโลเมตรจากจุด A จงหาความเร็วของการไหลของแม่น้ำ โดยสมมุติว่าเครื่องยนต์ทำงานคงที่
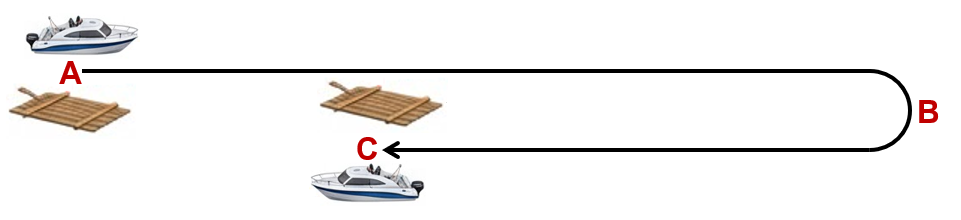
- แพไหลไปตามน้ำ ดังนั้น ความเร็วการไหลของแม่น้ำ = ความเร็วของแพ
- เมื่อเรือแล่นตามน้ำ ความเร็วเรือ = ความเร็วจากเครื่องยนต์ + ความเร็วแม่น้ำ
- เมื่อเรือแล่นทวนน้ำ ความเร็วเรือ = ความเร็วจากเครื่องยนต์ – ความเร็วแม่น้ำ
- โจทย์ข้อนี้ใช้สูตรเดียวคือ \(s=vt\) หรือ \(t = \dfrac{s}{v}\)
- โจทย์แนวๆนี้ปกติทำได้สองวิธีคือ ระยะทางเท่ากัน หรือ เวลาเท่ากัน
คำตอบ 3 km/hr หรือ \(\dfrac56\) m/s

- สมมุติ
- ความเร็วแม่น้ำเป็น \(v_f\)
- ความเร็วจากเครื่องยนต์เป็น \(v_e\)
- ระยะทางจาก A ไป C ให้เป็น \(s_{ac}\) = 6 km
- เวลาที่แพไหลจากจุด A ไป C เป็น \(t_{ac}\)
- เวลาที่เรือแล่นจาก A ไป B เป็น \(t_{ab}\) = 60 นาที
- เวลาที่เรือแล่นจาก B ไป C เป็น \(t_{bc}\)
- \(t_{ac} = \dfrac{s}{v_f}\)
- ระยะทางจาก A ไป B \(s_{ab} = \left(v_e + v_f\right)t_{ab}\)
- \(t_{bc} = \dfrac{s_{ab} – s_{ac}}{v_{bc}} = \dfrac{\left(v_e + v_f\right)t_{ab} – s}{v_e – v_f}\)
- เวลาที่แพไหลจากจุด A ไป C = เวลาที่เรือแล่นจาก A ไป B ไป C
- \(t_{ac} = t_{ab} + t_{bc}\) ดังนั้น
\begin{align} \dfrac{s_{ac}}{v_f} &= t_{ab} + \dfrac{\left(v_e + v_f\right)t_{ab} – s_{ac}}{v_e – v_f}\\ &= \dfrac{t_{ab}\left(v_e + v_f\right) + \left(v_e + v_f\right)t_{ab} – s_{ac}}{v_e – v_f}\\ &= \dfrac{2v_et_{ab} – s_{ac}}{v_e – v_f}\\ \dfrac{s_{ac}}{v_f} &= \dfrac{2v_et_{ab} – s_{ac}}{v_e – v_f}\\ s_{ac}\left(v_e – v_f\right) &= v_f\left(2v_et_{ab} – s_{ac}\right)\\ s_{ac}v_e &= v_f\times2v_et_{ab}\\ \therefore v_f &= \dfrac{s_{ac}}{2t_{ab}} \end{align}
แทนค่า \(s_{ac}\) = 6 km และ \(t_{ab}\) = 60 นาที = 1 ชม. จะได้ \(v_f\) = 3 km/hr หรือ \(\frac56\) m/s